これまでにカンファレンスなどで発表した資料をここにまとめます。 随時更新です。
最終更新: 2024-02-28
↓↓↓ 発表日降順で並んでいます
続きを読む9月末に福岡市の九大学研都市駅から佐賀県の唐津駅まで徒歩で移動する旅行をしました。ここに書き記します。
ざっくり 福岡市→糸島市→唐津市 をまたぐ道のりです。
全長36.7kmと表示されていますが、実際には42kmほどあります。(騙された)
九大学研都市駅から唐津駅まで JR 筑肥線が運行していて、かつ路線に沿って自動車道路が走っているので、その道をひたすら歩くことで唐津を目指しました。
歩きながら撮った写真を地図上にマッピングしてみました。地図上のマーカーを押下すると写真が見られます。
スマホだとめちゃくちゃ見づらいので PC 閲覧推奨です。








糸島市と唐津市の県境はひたすら海辺の風景でした。
昨年ダイエットのためにウォーキングを始めて、そのときから自分はひたすら歩くのが好きだし楽しいなと感じていました。 ただ同じ場所をグルグルと周回するだけでは飽きてしまうもので。目的地に向かって歩くのは新鮮で楽しいです。
また自分の足で歩いて旅をすることで、時間的にも空間的にも自分の身体のスケールでその道のりを体感できていいなーと感じました。
普段、家の近所を歩くときはビーチサンダルで歩き回っているので、今回も序盤はビーチサンダルを履いていました。
ビーチサンダルは軽くて歩きやすいのですが、かかとのクッション性は皆無なので着地の衝撃がもろにひざ・腰にきます。そのせいで10kmほど歩いた時点で腰が痛くなってきました。
腰に湿布を貼ってごまかしながら歩いていたら、今度は足首が痛くなってきました。
おそらく腰をかばうために腰全体を回すような歩き方になっていて、その負担が足首にかかって炎症を起こしました。
そんなわけで25kmをすぎたあたりから腰と足首を痛めて、片足を引きずるような歩き方でその後10km以上を歩きました。 立ち続け歩き続けているから炎症はひどくなっていく一方だし、とてもとてもツラかったです。
痛いながらに根性で歩き続けるのはまぁ可能なんですが。痛みが進行するほど歩く速度が遅くなっていって、結果として所要時間がどんどん伸びるのがツラい。
最終的に36kmほど歩いた地点でリタイアしました。
当初 Google マップを信じて約38kmほどの道のりだと思っていました。
が、GPS で自分の歩いた距離を測りながら進むと、残り距離の減り方がどうにも少ないことに気づきます。
18km歩いた地点で残りの距離を検索し直すと22kmと出ます。合計の道のりは40km?当初より増えている。
リタイアした36km地点での残り距離は8km。合計は44km。増えてんなぁ。
というわけで Google マップが示す2点間の距離はそれほど正確ではないようです。
まさか直線距離を出してはないと思うんですが、概算距離なのかな?
九大学研都市駅→唐津駅の距離は36.7kmと表示されますが、実際には42km以上あります。実際の距離が約2割ほど長いことを覚悟しておかないと心を折られかねませんね。
というわけで目指していた唐津駅まで辿り着けませんでした。
足の痛みでこれ以上歩けんーとなってリタイアしたんですが、時間的にも体力的にも余裕があったのでとても悔しいです。
痛みさえなければあと2時間ほど歩くのは苦ではなかったと思います。
というわけでそのうち再挑戦したいと思います。
まぁなんといってもビーチサンダルで10km歩いたのが無茶でしたね。ちゃんとかかとのクッションが効いたシューズを吐くのは大切。

...というわけで新しいシューズを買いました。
ニューバランスの専門店に行ったら計測もフィティングも丁寧で感激しました。
私ごとですが、体重が重すぎますね。
久しぶりに体重計に乗ったら86kg...。昨年ダイエットしたときは74kgまで落としたのにね。そら足腰に負担かかるわ。
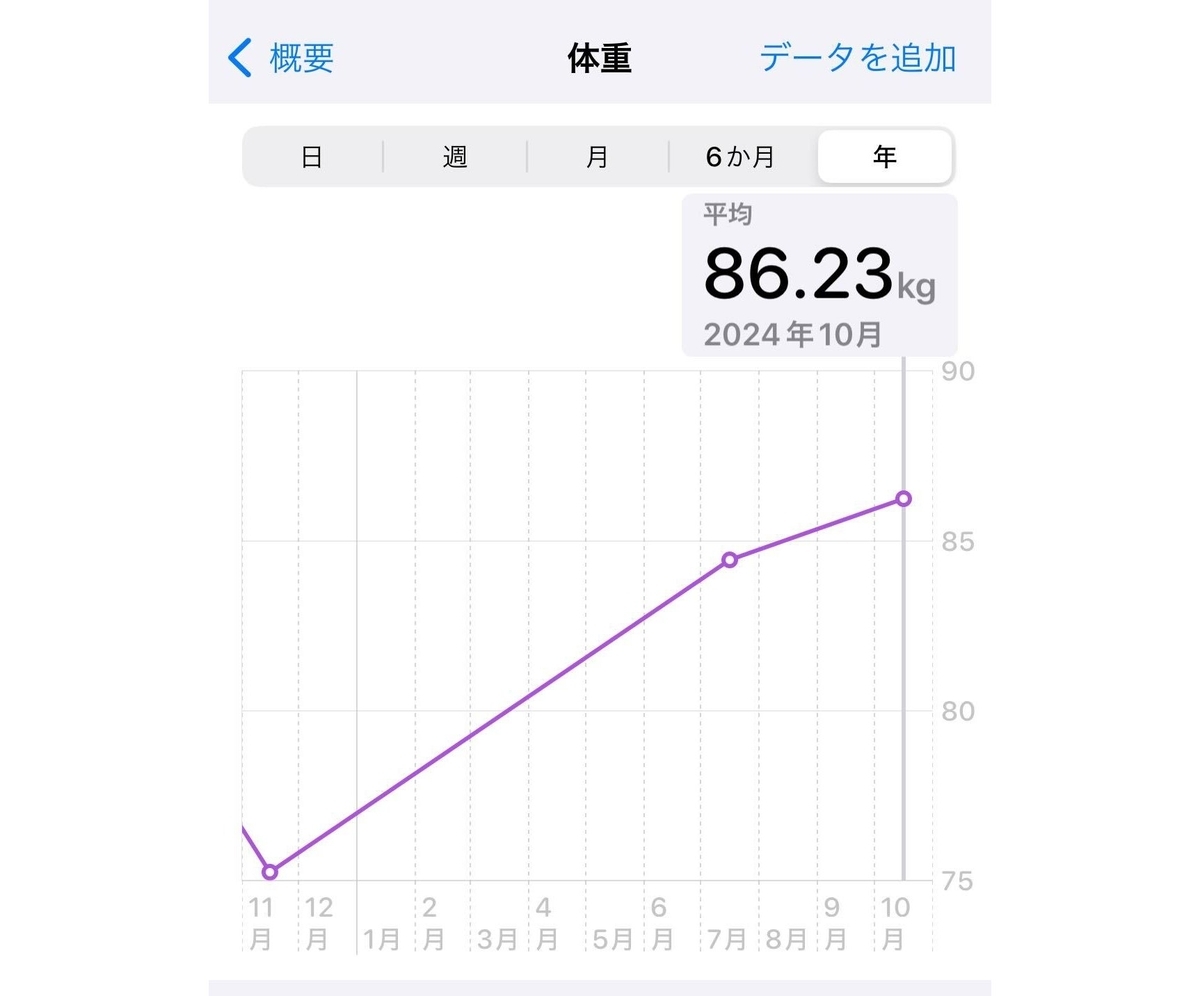
長距離歩くにあたってリュックの中身を精査したりするんですが。500mlのペットボトルを減らせば0.5kg減るのに対して12kg痩せれば12kg減りますからね。
というわけでダイエットをします。
関西圏を歩きで旅行したいなーと考えています。関西好きだし。
手始めに 姫路→神戸→梅田→京都市→大津→米原 とかの道のりはどうだろうと思って調べたら余裕で200km以上ありそうでした。
けどこの道のりを歩いていけたらたのしいだろうな。関西好きだし。
これからもがんばるぞ。
私からは以上です。

どうも、趣味で JavaScript を書いている三井です。
先日、 JavaScript つまみ食い LT 会 というイベントを主催しまして。 そのメインの LT 会後の懇親会で「懇親会 LT」と銘打ったゆるゆる LT をやりました。
私も参加して「JavaScript で Hello,world! に挑戦」という話をしたんですが、その資料が Web に上がっていないので (というか資料無しで話したので) この場を借りて話した内容をまとめてみます。
ブラウザに Hello,world! を表示させる JavaScript プログラムを 記号だけ を使って書きます。
プログラムを学び始めた人がまず最初に取り組む課題が Hello,world! を表示するだけのプログラムを書くというもの。
いまいちど初心に立ち返って記号だけで Hello,world! を書けば、 JavaScript についてより深く知ることができるんじゃないでしょうか(適当)
この JavaScript 記号プログラミングは散々語り尽くされた分野です。
パイプライン演算子 |> を取り入れたこれからの記号プログラミングみたいな目新しい話題は出てきません。
それでもいいよという方だけご笑納ください。
では、さっそく取り組んでいきましょう。
まずは記号だけで何ができるのか軽く素振りして確認してみましょう。
おなじみの空配列は、
[]
+ 演算子をつけることで数として評価されて、
+[] // 0
このように 0 に化けます。
また、~ 演算子で補数を取ると、
~[] // -1
0 以外の数を作ることができます。
なので、
+[] // 0 ~[] // -1 -~[] // 1 ~-~[] // -2 -~-~[] // 2 ~-~-~[] // -3 ...
このように任意の整数を作ることができます。
続いて、
先ほどの空配列 [] を ! 演算子で論理反転させると、
![] // false !![] // true
true と false が得られました。
さらに、 true と false を空文字列 '' と結合すれば、
''+ ![] // 'false' ''+!![] // 'true'
文字列としての 'true' と 'false' が得られました。
整数と文字列が手に入ったので、文字列を演算してみます。
ご存知の通り、
'false'[1] // 'a'
ですので、
(''+![])[-~[]] // 'a'
このように書くことで文字列の 'a' を取り出すことができました。
いかがでしょう。記号フログラミングの大いなる可能性を感じていただけましたね?
では Hello,world! しましょう。
まずは普通に、
alert('Hello,world!')
これを変形していきます。
使えるものが記号しかない都合上、ほとんどの組み込み関数はそのまま使うことができません。
なので eval() を使って書き直します。
eval("alert('Hello,world!')")
eval() はプログラムを 文字列として 与えてやればなんでも実行してくれる心強いやつです。
ですが、記号プログラミングでは eval() すら自由に使うことができません。代わりに関数コンストラクタ Function() で置き換えます。
Function("alert('Hello,world!')")()
関数コンストラクタ Function() は文字列を与えてインスタンス化すると eval() 相当の働きをする関数を返してくれます。
しかも new 演算子をつけずに関数として呼び出したときにも new 演算子でインスタンス化したときと同様に振る舞うという 雑な 力強い仕様です。
Function() を調達するFunction() をどこからともなく持ってきましょう。
空配列 [] の constructor を参照してみます。
[].constructor // function Array() { [native code] }
もういっちょ
[].constructor.constructor // function Function() { [native code] }
というわけで空配列 [] から Function() を得ることができました。
上記をふまえて alert('Hello,world!') は
[].constructor.constructor("alert('Hello,world!')")()
というように変形できます。
さらにさらにメソッド呼び出しをドット演算子 . からブラケット記法 [] に置き換えておきます。
[]['constructor']['constructor']("alert('Hello,world!')")()
これです。
プログラムの中に 記号と文字列しかない 状態にまで変形できたことがお分りでしょうか。
と言うわけで、残る文字列部分を記号に置き換えていきたいんですが。
その前に、よく登場するフレーズを変数に入れて用意しておきましょう。
まずは 'constructor' を。
(''+{})[-~-~-~-~-~[]] // c +(''+{})[-~[]] // o +(''+[][[]])[-~[]] // n +(''+![])[-~-~-~[]] // s +(''+!![])[+[]] // t +(''+!![])[-~[]] // r +(''+[][[]])[+[]] // u +(''+({}))[-~-~-~-~-~[]] // c +(''+!![])[+[]] // t +(''+({}))[-~[]] // o +(''+!![])[-~[]] // r
このように記号化して変数に入れます。
記号の中で変数名として使えるのは $ と _ ですね。
'constructor' を _ に代入します。
_=(''+{})[-~-~-~-~-~[]]+(''+{})[-~[]]+(''+[][[]])[-~[]]+(''+![])[-~-~-~[]]+(''+!![])[+[]]+(''+!![])[-~[]]+(''+[][[]])[+[]]+(''+({}))[-~-~-~-~-~[]]+(''+!![])[+[]]+(''+({}))[-~[]]+(''+!![])[-~[]]
はい。
次、 Function() を _$ に代入します。
_$=[][_][_]
簡単ですね。
それから、気まぐれに 'return "\u' を用意して、
(''+!![])[-~[]] // r +(''+!![])[-~-~-~[]] // e +(''+!![])[+[]] // t +(''+!![])[-~-~[]] // u +(''+!![])[-~[]] // r +(''+[][[]])[-~[]] // n +(''+{})[-~-~-~-~-~-~-~[]] // ' ' +'"\\' // "\ +(''+[][[]])[+[]] // u
変数 __ に代入します。
__=(''+!![])[-~[]]+(''+!![])[-~-~-~[]]+(''+!![])[+[]]+(''+!![])[-~-~[]]+(''+!![])[-~[]]+(''+[][[]])[-~[]]+(''+{})[-~-~-~-~-~-~-~[]]+'"\\'+(''+[][[]])[+[]]
これで役者は揃いました。
ではいよいよ、
[]['constructor']['constructor']("alert('Hello,world!')")()
を記号だけで置き換えて、
// 'constructor' _=(''+{})[-~-~-~-~-~[]]+(''+{})[-~[]]+(''+[][[]])[-~[]]+(''+![])[-~-~-~[]]+(''+!![])[+[]]+(''+!![])[-~[]]+(''+[][[]])[+[]]+(''+({}))[-~-~-~-~-~[]]+(''+!![])[+[]]+(''+({}))[-~[]]+(''+!![])[-~[]] // Function() _$=[][_][_] // 'return "\u' __=(''+!![])[-~[]]+(''+!![])[-~-~-~[]]+(''+!![])[+[]]+(''+!![])[-~-~[]]+(''+!![])[-~[]]+(''+[][[]])[-~[]]+(''+{})[-~-~-~-~-~-~-~[]]+'"\\'+(''+[][[]])[+[]] // alert('Hello,world!') // -> eval("alert('Hello,world!')") // -> Function("alert('Hello,world!')")() // -> []['constructor']['constructor']("alert('Hello,world!')")() [][ _ // 'constructor' ][ _ // 'constructor' ]( (''+![])[-~[]] // a +(''+![])[-~-~[]] // l +(''+![])[-~-~-~-~[]] // e +(''+!![])[-~[]] // r +(''+!![])[+[]] // t +"('" // (' +_$(__+(+[])+(+[])+(-~-~-~-~[])+(-~-~-~-~-~-~-~-~[])+'"')() // H +(''+!![])[-~-~-~[]] // e +(''+![])[-~-~[]] // l +(''+![])[-~-~[]] // l +(''+{})[-~[]] // o +',' // , +_$(__+(+[])+(+[])+(-~-~-~-~-~-~-~[])+(-~-~-~-~-~-~-~[])+'"')() // w +(''+({}))[-~[]] // o +(''+!![])[-~[]] // r +(''+![])[-~-~[]] // l +(''+[][[]])[-~-~[]] // d +_$(__+(+[])+(+[])+(-~-~[])+(-~[])+'"')() // ! +"')" // ') )()
さらに minify して、
_=(''+{})[-~-~-~-~-~[]]+(''+{})[-~[]]+(''+[][[]])[-~[]]+(''+![])[-~-~-~[]]+(''+!![])[+[]]+(''+!![])[-~[]]+(''+[][[]])[+[]]+(''+({}))[-~-~-~-~-~[]]+(''+!![])[+[]]+(''+({}))[-~[]]+(''+!![])[-~[]];_$=[][_][_];__=(''+!![])[-~[]]+(''+!![])[-~-~-~[]]+(''+!![])[+[]]+(''+!![])[-~-~[]]+(''+!![])[-~[]]+(''+[][[]])[-~[]]+(''+{})[-~-~-~-~-~-~-~[]]+'"\\'+(''+[][[]])[+[]];[][_][_]((''+![])[-~[]]+(''+![])[-~-~[]]+(''+![])[-~-~-~-~[]]+(''+!![])[-~[]]+(''+!![])[+[]]+"('"+_$(__+(+[])+(+[])+(-~-~-~-~[])+(-~-~-~-~-~-~-~-~[])+'"')()+(''+!![])[-~-~-~[]]+(''+![])[-~-~[]]+(''+![])[-~-~[]]+(''+{})[-~[]]+','+_$(__+(+[])+(+[])+(-~-~-~-~-~-~-~[])+(-~-~-~-~-~-~-~[])+'"')()+(''+({}))[-~[]]+(''+!![])[-~[]]+(''+![])[-~-~[]]+(''+[][[]])[-~-~[]]+_$(__+(+[])+(+[])+(-~-~[])+(-~[])+'"')()+"')")()
完成です!

はい、
お疲れさまでした。
ここまで読み進められた方ならば JavaScript の記号プログラミングの魅力を少しでも感じ取っていただけたんではないでしょうか。
私からは以上です。
実は今回のような制限の中でプログラムを書く遊びは言語を問わずに様々にあるものでして。
例えば Ruby でも記号だけを使ったプログラムが可能です。
私が知る限りこのような遊びの中でも古いものに perl の 予約語 だけを使ったプログラムがあります。
ppencode というキーワードで検索するといろいろな記事が見つかると思います。
ppencode 発案者は @TAKESAKO さんという方で、自らが ppencode について解説したセッションが動画で残っているので興味のある方はぜひ見てみてください。
perl が読めない書けない人でも ppencode の面白さ・ワクワク感が伝わってくる良いセンションだと思います。
それでは、Enjoy!! ;)
この記事は私 id:todays_mitsui が都内某所に寄稿していた記事です。
寄稿した先のブログがすっかり消されているのを見たので、ここに再掲します。
GitHub Actions から AWS などのリソースに安全にアクセスするためには OIDC (OpenID Connect) という仕組みを利用します。
...ということを見聞きしてさらっと知ってはいたのですが、自分で一通りの設定をなぞってやったことはなかったのでやってみます。
OIDC を使うのが主流 (メジャー) だから。
というのは冗談で、
OICD で使う ID トークンは短命で、万が一漏洩しても被害を最小限に抑えられるとのことです。
また AssumeRole の仕組みを使うことでアクセス元を ユーザー/リポジトリ/ブランチ まで細かく絞れるのがいい感じだなと思いました。
まずは AWS コンソール側であれこれ準備をします。
練習なので何もリソースを作っていない真っさらなアカウントを用意しました。

IAM > ID プロバイダ から ID プロバイダを追加します。
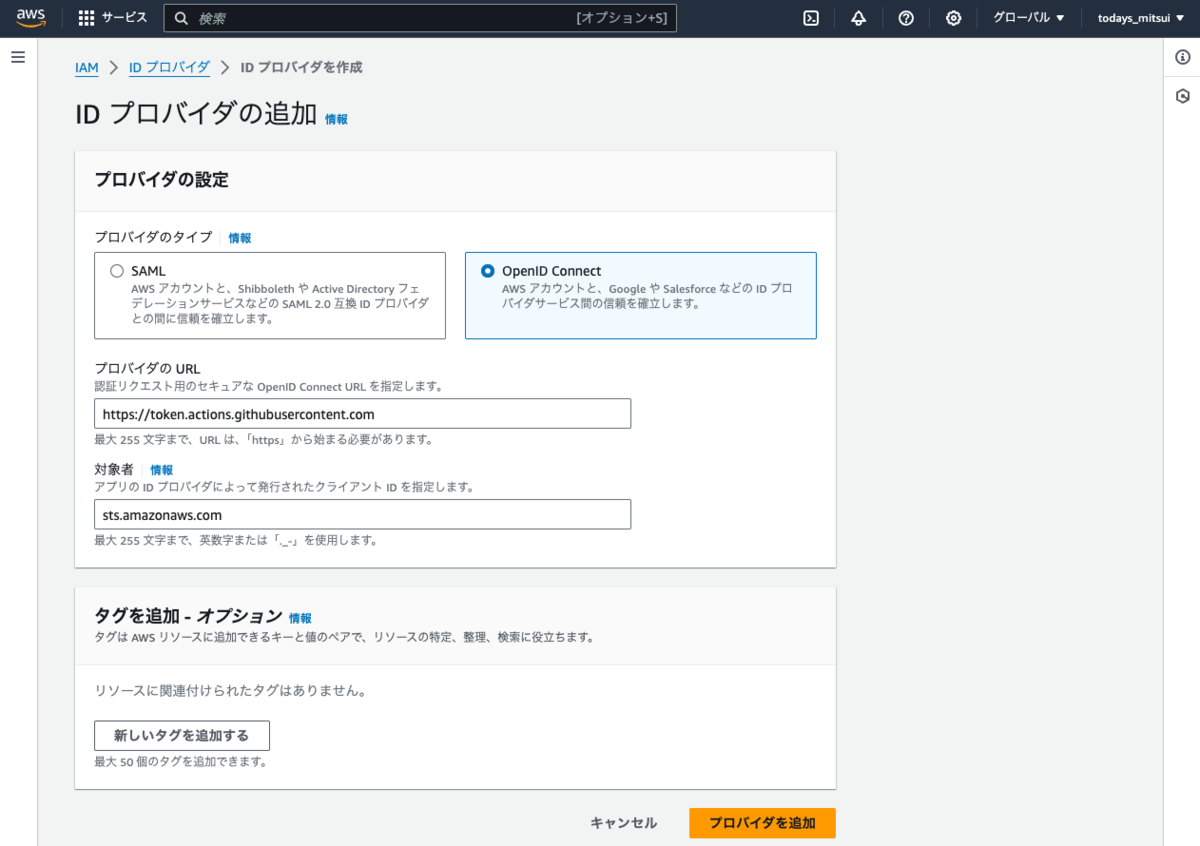
次に IAM > ロール からロールを作成。
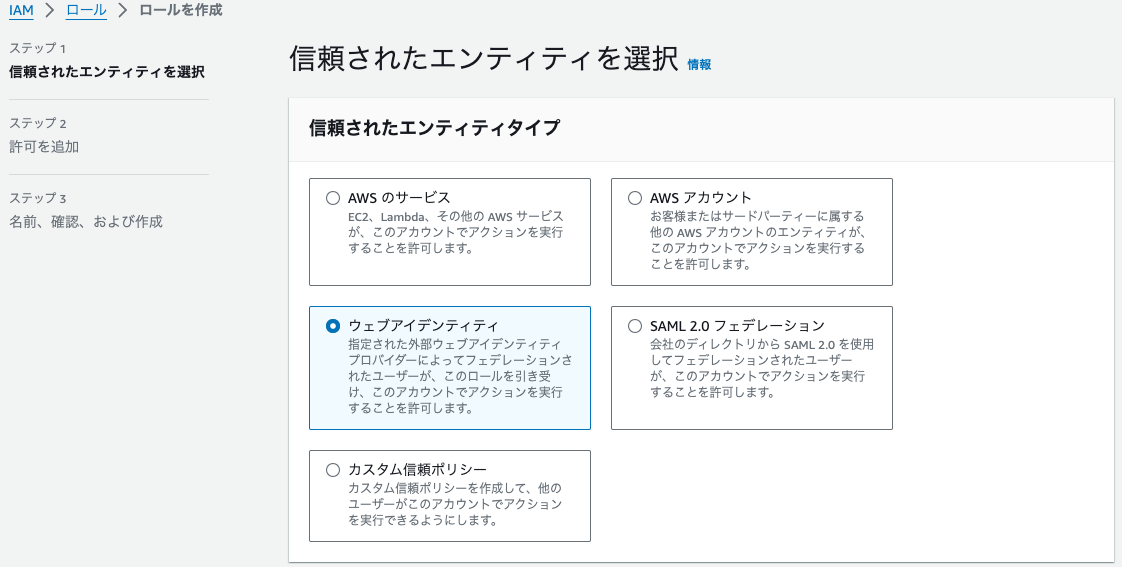

先ほど作成したプロバイダ token.actions.githubusercontent.com が選択肢に表示されているので選択します。これにて ID プロバイダと IAM ロールが紐付きます。
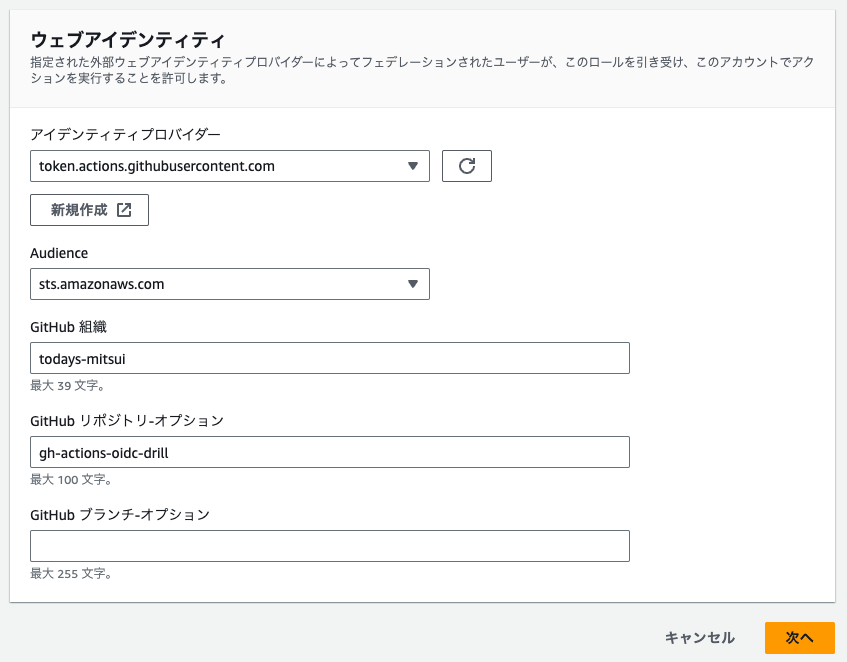
リソースへのアクセスを許したい「GitHub 組織」「GitHub リポジトリ」「GitHub ブランチ」をそれぞれ設定します。
リポジトリとブランチの設定は任意なので空欄のままでも可ですが、アクセス元の制御が緩くなるので GitHub 側の設定を誤ったときにより脆弱になります。
組織設定を誤ると他のユーザーからのアクセスを許すことになるのでセキュリティホールになります。
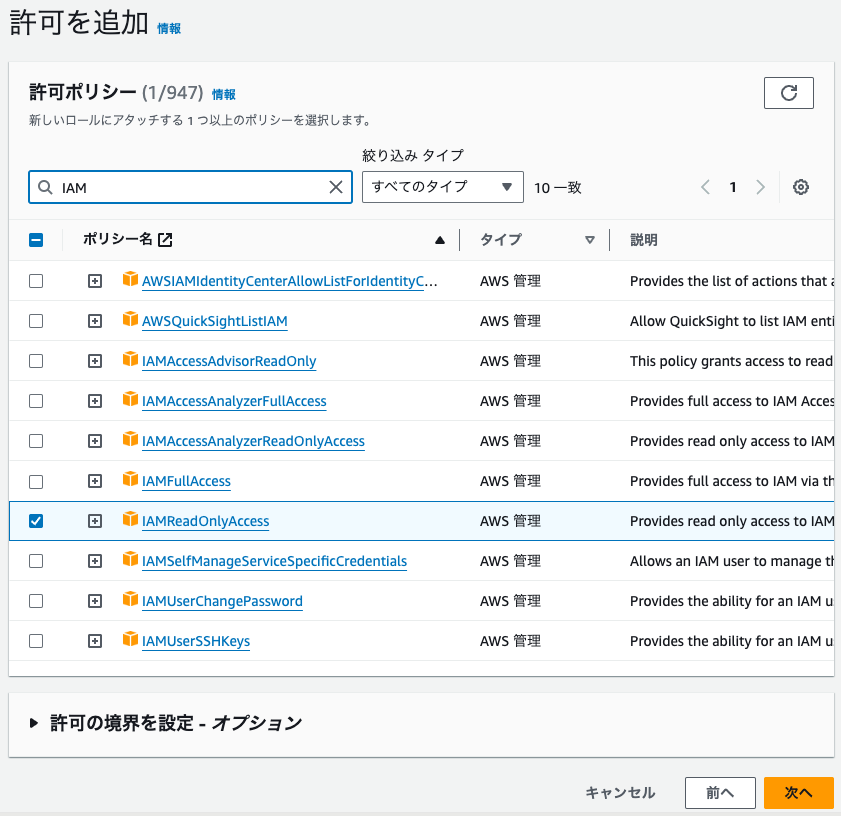
ポリシーをアタッチしてこのロールで可能な操作を決めます。ロール作成後に変更可能なのでいったん IAMReadOnlyAccess だけつけておきます。
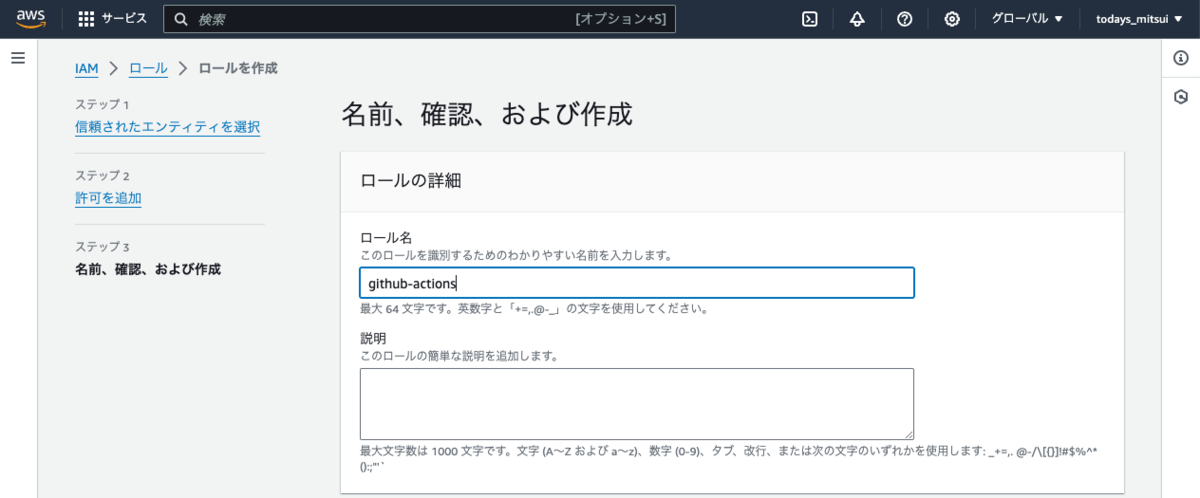
分かりやすいロール名を設定して完了です。
作成したロールを見てみましょう。
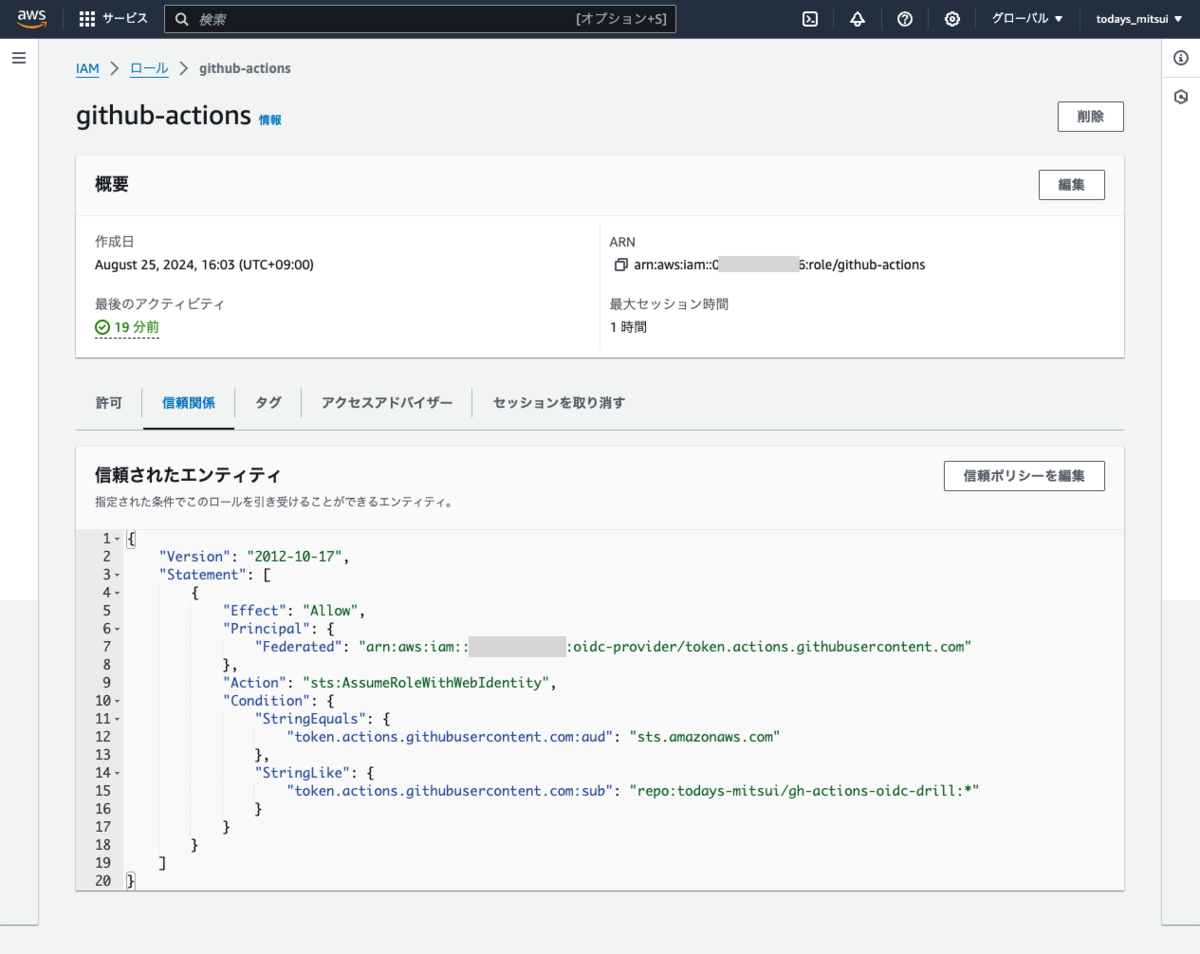
「信頼関係」というタブにアクセス元の制御が JSON で書かれています。
{ "Statement" { "Condition" { "StringLike" {"token.actions.githubusercontent.com:sub": "..." } } } } の内容によってどの組織のどのリポジトリのどのブランチからのアクセスを許可するか決まります。
ここを細かく書き換えることで特定のブランチからのみアクセスを許可するなどの細かな制御が可能です。
ここまでで AWS コンソール側での一通りの準備が完了しました。
以上をやりました。
todays-mitsui/gh-actions-oidc-drill というリポジトリを作って GitHub Actions のワークフローを書いていきます。
.github/workflows/open-id-connect.yaml というファイルを作成します。
name: OpenID Connect on: push env: ROLE_ARN: arn:aws:iam::${{ secrets.AWS_ID }}:role/${{ secrets.ROLE_NAME }} SESSION_NAME: gh-oidc-${{ github.run_id }}-${{ github.run_attempt }} jobs: connect: timeout-minutes: 5 runs-on: ubuntu-latest permissions: id-token: write steps: - uses: aws-actions/configure-aws-credentials@v4 with: role-to-assume: ${{ env.ROLE_ARN }} role-session-name: ${{ env.SESSION_NAME }} aws-region: ap-northeast-1 - run: aws iam list-users - run: aws iam create-user --user-name invalid || true
aws-actions/configure-aws-credentials というアクションを使って OIDC の認証を行います。
認証に成功すれば AWS_SESSION_TOKEN などの環境変数がセットされます。以降は aws コマンドで環境変数を読んで適切な権限でリソースにアクセスすることが可能です。
さて、さっそく実行してみたいところですが、 ROLE_ARN: arn:aws:iam::${{ secrets.AWS_ID }}:role/${{ secrets.ROLE_NAME }} の部分がシークレットで一部隠されています。
ワークフローの実行前に GitHub リポジトリの Settings > Secrets and variables > Actions の画面から適切に値を設定しておく必要があります。
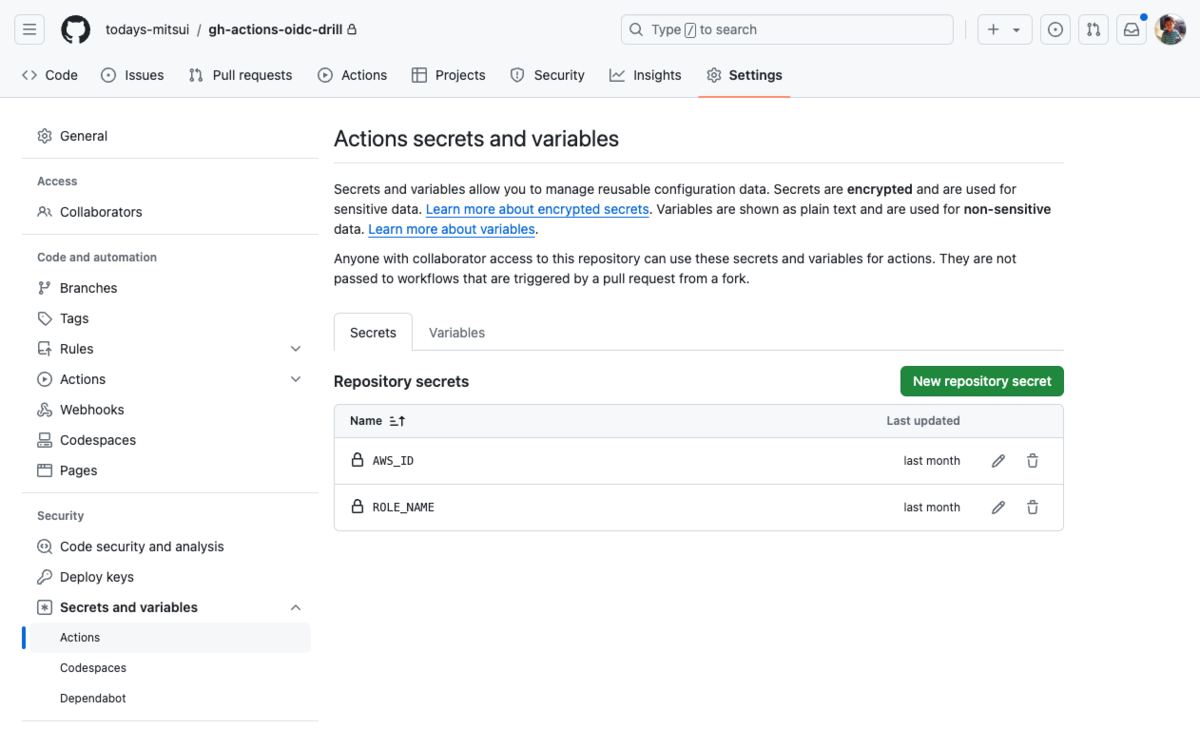
AWS_ID は AWS コンソールの右上で確認できる「アカウント ID」のハイフンを抜いた数字列を、ROLE_NAME は先ほど作成した IAM ロールの名前 (今回の例では github-actions) を設定します。
実行してみましょう。実際のログが ここ から見られます。
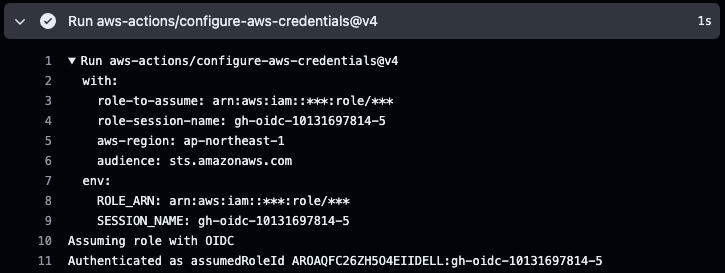
aws-actions/configure-aws-credentials@v4 のステップで正常に認証が行われています。
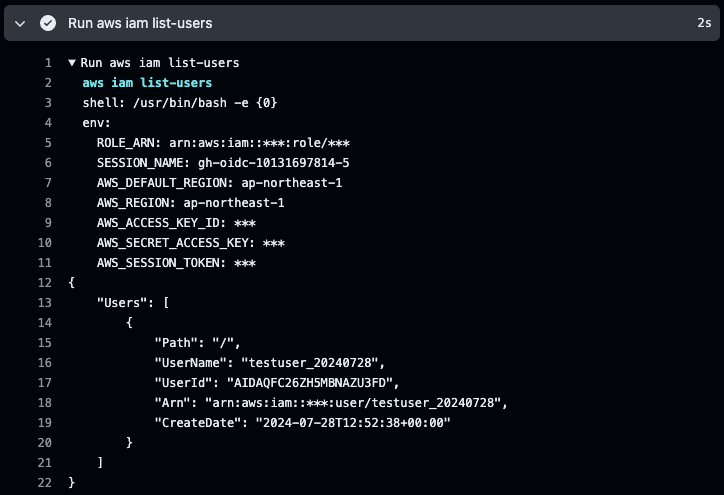
その後 aws iam list-users のステップでリソースにアクセスして IAM ユーザーの一覧情報が取得できました。
実行確認のために作成したテストユーザーの情報が見えています。
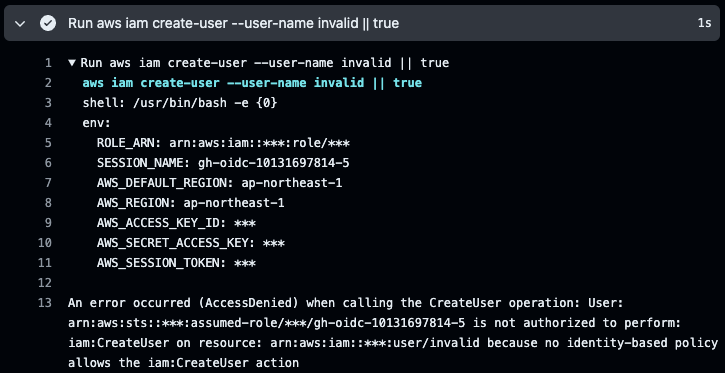
さらに次のステップでは aws iam create-user しようとして失敗しています。
使用している IAM ロールにアタッチしたポリシーは IAMReadOnlyAccess で、ユーザーを作成する権限が無いためです。
アタッチした以上の強すぎる権限は発揮できないことが確認できました。
今回作成した ID プロバイダと IAM ロールでは todays-mitsui/gh-actions-oidc-drill リポジトリからのみリソースにアクセスできるように設定しました。
ということは別のリポジトリ (例えば todays-mitsui/gh-actions-oidc-drill-another リポジトリ) からはアクセスできないはずです。
todays-mitsui/gh-actions-oidc-drill-another というリポジトリを作り、同じ内容の .github/workflows/open-id-connect.yaml ファイルを置いてワークフローを実行してみましょう。
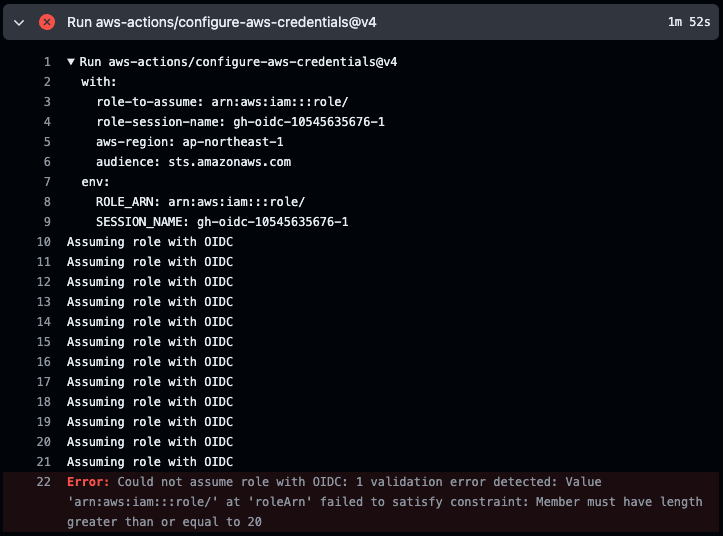
はい、何度かリトライした後に認証に失敗してエラーになっています。
リポジトリのオーナーはどちらも私 (todays-mitsui) ですが、リポジトリ単位でアクセス許可の制御ができました。
最初は AWS コンソールでの設定が面倒かなと思いましたが、意外と最低限の必要事項だけで設定できるので内容の理解は容易です。
GitHub Actions のワークフローファイルに一切の機密情報を置くことなくアクセス制御ができるのが安心・便利ですね。
さて次回もまた GitHub Actions の便利な機能を試します。GitHub Apps トークンを使ってリポジトリを跨いだアクセス制御に挑戦しようと思います。
私からは以上です。